The equations of motion for tall
![]() fingers were first derived by Stern (1960)
fingers were first derived by Stern (1960)
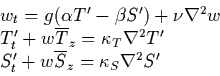 |
(1) |
Solutions to the above equations can be found of square planform
![]() sheet planform
sheet planform
![]() or a combination of the two that can take the form of triangles, hexagons
or asymmetric plumes (Schmitt 1994). Here,
or a combination of the two that can take the form of triangles, hexagons
or asymmetric plumes (Schmitt 1994). Here, ![]() is the growth rate, and kx and ky are horizontal wavenumbers. Growth rates
is the growth rate, and kx and ky are horizontal wavenumbers. Growth rates ![]() are positive for
density ratios
are positive for
density ratios
![]() (Huppert and Manins 1973) and horizontal
wavenumbers k
(Huppert and Manins 1973) and horizontal
wavenumbers k
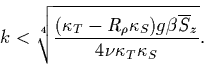 |
(2) |
(Fig. 1). Growth rates increase as density ratios ![]() approach 1. For any
given density ratio
approach 1. For any
given density ratio ![]() ,
maximum growth rates occur at intermediate
wavelengths (dashed curve) due to competition between destabilizing heat
diffusion and viscous drag both which become stronger at smaller scales.
,
maximum growth rates occur at intermediate
wavelengths (dashed curve) due to competition between destabilizing heat
diffusion and viscous drag both which become stronger at smaller scales.
Figure 2 displays the ratio of heat- to salt-flux contributions to
buoyancy-flux
![]() as a function of density ratio
as a function of density ratio ![]() and horizontal wavelength
and horizontal wavelength
![]() .
Heat-salt laboratory experiments corrected for molecular
diffusion of heat through the interface and tank sidewalls typically find flux
ratios of 0.5-0.65 (Fig. 3; Turner 1967; Schmitt 1979a; Taylor and
Bucens 1989; Shen 1993), consistent with fastest-growing finger flux ratios
or fingers of maximum velocity, though McDougall and Taylor (1984) and
Linden (1973) both reported lower values, more consistent with steady
fingers. Schmitt et al. (1987) inferred flux ratios of 0.85 in the
thermohaline staircase east of Barbados based on the lateral density ratio of
the homogeneous layers. These were argued to be a combination of fastest-
growing finger flux ratio and either (i) turbulence with
.
Heat-salt laboratory experiments corrected for molecular
diffusion of heat through the interface and tank sidewalls typically find flux
ratios of 0.5-0.65 (Fig. 3; Turner 1967; Schmitt 1979a; Taylor and
Bucens 1989; Shen 1993), consistent with fastest-growing finger flux ratios
or fingers of maximum velocity, though McDougall and Taylor (1984) and
Linden (1973) both reported lower values, more consistent with steady
fingers. Schmitt et al. (1987) inferred flux ratios of 0.85 in the
thermohaline staircase east of Barbados based on the lateral density ratio of
the homogeneous layers. These were argued to be a combination of fastest-
growing finger flux ratio and either (i) turbulence with
![]() (Marmorino 1990; Fleury and Lueck 1991) or nonlinearity in the seawater
equation of state influencing the flux divergence (McDougall 1991).
(Marmorino 1990; Fleury and Lueck 1991) or nonlinearity in the seawater
equation of state influencing the flux divergence (McDougall 1991).
Theoretical fingering studies have focussed on fastest-growing, steady and spectral descriptions of finger dynamics. Fastest-growing investigations (Stern 1975; Schmitt 1979b; Kunze 1987) have been justified by the close match between the fastest-growing flux ratio and that found in the laboratory and numerical simulations (Fig. 3) as well as the expected long-time dominance of fastest-growing fingers. The spectral approach recognizes that a range of scales is likely to be present, and that fingers may break down due to secondary instability before fastest-growing fingers dominate, particularly at low density ratio (Gargett and Schmitt 1982; Shen and Schmitt 1995).
Steady models have been applied to thin interfaces sandwiched
between homogeneous layers on the grounds that, because of the interface's
finite thickness li and salinity step ![]() ,
these are expected to
evolve quickly to steady state (Huppert and Manins 1973; Stern 1976; Joyce
1982; Howard and Veronis 1987; 1992). Stern (1976) examined the
solution to the steady equations, choosing the wavenumber
,
these are expected to
evolve quickly to steady state (Huppert and Manins 1973; Stern 1976; Joyce
1982; Howard and Veronis 1987; 1992). Stern (1976) examined the
solution to the steady equations, choosing the wavenumber
![$[g\alpha \overline{T}_z/(4\nu \kappa _T)]^{1/4}$](img26.gif) that produced the maximum buoyancy-flux for a given
that produced the maximum buoyancy-flux for a given 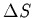 .
The
associated flux ratio was 0.2-0.25. Howard and Veronis (1987) examined
the structure of steady fingers of maximum buoyancy-flux extending
between two homogeneous reservoirs in the limit of very small salt
diffusivity
.
The
associated flux ratio was 0.2-0.25. Howard and Veronis (1987) examined
the structure of steady fingers of maximum buoyancy-flux extending
between two homogeneous reservoirs in the limit of very small salt
diffusivity
![]() ,
obtaining similarity solutions for the
boundary layers between adjacent fingers. They again found flux ratios of
,
obtaining similarity solutions for the
boundary layers between adjacent fingers. They again found flux ratios of
![]() associated with the wavenumber of maximum buoyancy-flux.
Howard and Veronis (1992) examined the stability of these fingers as a
function of a nondimensionalized salinity step, or finger aspect ratio,
associated with the wavenumber of maximum buoyancy-flux.
Howard and Veronis (1992) examined the stability of these fingers as a
function of a nondimensionalized salinity step, or finger aspect ratio,
![]() where
where
![]() is the buoyancy-layer scale. They found that the dominant instability
switched from being oscillatory involving viscosity and heat diffusivity for
is the buoyancy-layer scale. They found that the dominant instability
switched from being oscillatory involving viscosity and heat diffusivity for
![]() to pure real and due to shear between adjacent fingers
to pure real and due to shear between adjacent fingers
![]() at higher Q.
at higher Q.
Relaxing the condition that the fingers be tall and thin (e.g., Howard
and Veronis 1987), additional terms must be included such as the vertical
pressure gradient pz in the vertical momentum equation, vertical
diffusion
![]() ,
and horizontal advection of temperature and
salinity, particularly at the finger tips. These additional terms could play
an important role at low density ratios, where fingers are short and stubby
rather than tall and thin (Howard and Veronis 1987), or for fingers
evolving in a thin high-gradient interfaces sandwiched between two
homogeneous layers as characterizes most lab and numerical experiments.
Numerical simulations under these conditions show formation of bulbous
tips where the fingers intrude into the adjacent homogenous layers (Fig. 4;
Shen 1989; Shen and Veronis 1996). The resulting structure depends on
the destabilizing salinity step across the interface
,
and horizontal advection of temperature and
salinity, particularly at the finger tips. These additional terms could play
an important role at low density ratios, where fingers are short and stubby
rather than tall and thin (Howard and Veronis 1987), or for fingers
evolving in a thin high-gradient interfaces sandwiched between two
homogeneous layers as characterizes most lab and numerical experiments.
Numerical simulations under these conditions show formation of bulbous
tips where the fingers intrude into the adjacent homogenous layers (Fig. 4;
Shen 1989; Shen and Veronis 1996). The resulting structure depends on
the destabilizing salinity step across the interface ![]() as well as the
density ratio
as well as the
density ratio ![]() .
Presumably, there is also a dependence on the thickness of
the high-gradient interface li.
.
Presumably, there is also a dependence on the thickness of
the high-gradient interface li.
In the remainder of this section on salt-finger theory, attention will be focussed on fastest-growing fingers because the fastest-growing flux ratio is found in lab and numerical simulations (Fig. 3), because thin interfaces for which fingers might be expected to extend from one reservoir to the next do not appear to be realized in the ocean, and because numerical models do not achieve a steady state except in a statistical sense (Shen 1993; 1995). Shen (1993) demonstrated that steady fingers of maximum-buoyancy-flux wavenumber could not reproduce the lab and numerical flux ratios, regardless of the degree of salt diffusion between adjacent fingers. He showed that choosing the wavenumber associated with maximum velocity across an interface produced flux ratios in the observed range. Maximum velocity fingers closely resemble fastest-growing.
a. fastest-growing fingers
Theory readily identifies the fastest-growing salt-fingering wavenumber
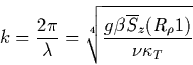 |
(3) |
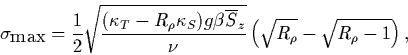 |
(4) |
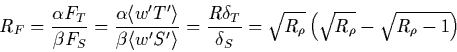 |
(5) |
b. fluxes
Quantifying the fingering heat- and salt-fluxes of relevance to the
general oceanographic community is more difficult, requiring knowledge
of what limits the growth of fingers to finite amplitude. This was
originally attempted through laboratory experiments in which the heat- and
salt-fluxes were measured between two well-mixed layers separated by a
thin fingering-favorable interface (Turner 1967; Linden 1973; Schmitt
1979a; McDougall and Taylor 1984; Taylor and Bucens 1989). The heat-
and salt-fluxes were found to depend only on the salinity step across the
interface ![]() and the density ratio
and the density ratio ![]()
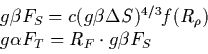 |
(6) |
Dimensional arguments were also used by Stern (1969) to argue that
the ratio of the buoyancy-flux
![]() to
to ![]() is limited to a
maximum value
is limited to a
maximum value
| (7) |
Kunze (1987) suggested that finger growth could be limited by secondary instability when a finger Froude number
| (8) |
![\begin{displaymath}\begin{array}{l}
g\alpha F_T = g\alpha\langle w'T'\rangle =
...
...\left(\sqrt{R_\rho}+\sqrt{R_\rho-1}\right)^2\right]
\end{array}\end{displaymath}](img53.gif) |
(9) |
![\begin{displaymath}\sigma t_{\mbox{\scriptsize {\rm max}}}=ln\left[
\sqrt{\frac{...
...-1}}
\left(\sqrt{R_\rho}+
\sqrt{R_\rho-1}\right)^{3/2}\right].
\end{displaymath}](img54.gif) |
(10) |
Assuming that the salinity step ![]() is defined by the maximum attained
height
is defined by the maximum attained
height
![]() of the fingers, that is, equating the high-gradient interface
thickness li and maximum finger height
of the fingers, that is, equating the high-gradient interface
thickness li and maximum finger height
![]() ,
the Stern or finger Froude
number constraints reproduce laboratory
,
the Stern or finger Froude
number constraints reproduce laboratory
![]() flux laws except for density
ratios
flux laws except for density
ratios
![]() where fluxes are underpredicted by factors of 2-3 (Figs. 7
and 8; Kunze 1987; Shen 1993). This criterion implies interface
thicknesses
where fluxes are underpredicted by factors of 2-3 (Figs. 7
and 8; Kunze 1987; Shen 1993). This criterion implies interface
thicknesses ![]() (0.1 m), an order of magnitude smaller than the 2-5 m
thickness typically observed in oceanic staircases. Shen (1993) argued that
comparison of Kunze's gradient formulation with lab measurements was
inappropriate because lab fingers extend across the entire interface so are
fed by homogeneous reservoirs. However, his numerical simulations
showed little sensitivity to whether the horizontal salinity structure was a
square wave or a sine wave.
(0.1 m), an order of magnitude smaller than the 2-5 m
thickness typically observed in oceanic staircases. Shen (1993) argued that
comparison of Kunze's gradient formulation with lab measurements was
inappropriate because lab fingers extend across the entire interface so are
fed by homogeneous reservoirs. However, his numerical simulations
showed little sensitivity to whether the horizontal salinity structure was a
square wave or a sine wave.
c. staircase lengthscales
With a dependence on the salinity gradient
![]() across the interface
(9), oceanic fingering fluxes depend both on the layer thickness Lo, which
establishes the interfacial salinity step
across the interface
(9), oceanic fingering fluxes depend both on the layer thickness Lo, which
establishes the interfacial salinity step
![]() given a
largescale smoothed salinity gradient
given a
largescale smoothed salinity gradient
![]() ,
and the
interface thickness li which determines the interfacial gradient
,
and the
interface thickness li which determines the interfacial gradient
![]() for
for
![]() .
.
What controls layer and interface staircase thicknesses in the ocean is not known. While staircase formation has traditionally been thought of as a 1-D instability induced by the countergradient double-diffusive buoyancy-fluxes based on lab studies (Stern and Turner 1969), it may also arise from horizontal interleaving processes (ref. appropriate section) which may also explain the alternating diffusive and fingering layers that extend across entire basins in the Arctic Ocean, crossing different water- masses and water ages with impunity (Carmack et al. 1998).
Given the persistence and invariance of oceanic thermohaline
staircase T, S structures over at least 25 years (Schmitt 1995), staircases
have more than enough time to establish thin
![]() flux law interfaces. A
range of interface thicknesses were found in the thermohaline staircase east
of Barbados, including a few of O(0.1 m). However, the bulk of the
interfaces were 2-5 m thick, an order of magnitude too large for
flux law interfaces. A
range of interface thicknesses were found in the thermohaline staircase east
of Barbados, including a few of O(0.1 m). However, the bulk of the
interfaces were 2-5 m thick, an order of magnitude too large for
![]() flux laws to apply.
flux laws to apply.
Kelley's (1984) scaling for layer thickness
![]() and diffusivity
and diffusivity
![]() appears to work well for diffusively-unstable staircases. One might blindly replace
the molecular diffusivity of heat
appears to work well for diffusively-unstable staircases. One might blindly replace
the molecular diffusivity of heat ![]() with the fingering salt diffusivity
with the fingering salt diffusivity
![]() .
However, using observed microstructure
estimates of the salt-flux (Gregg and Sanford 1987; Lueck 1987) then underestimates
the layer thicknesses. Interestingly, a laboratory
.
However, using observed microstructure
estimates of the salt-flux (Gregg and Sanford 1987; Lueck 1987) then underestimates
the layer thicknesses. Interestingly, a laboratory
![]() salt-flux (6)
produces layer thicknesses of the right order of magnitude.
salt-flux (6)
produces layer thicknesses of the right order of magnitude.
d. differing fluxes in the lab and ocean
Why are oceanic fluxes so much weaker, or equivalently, oceanic
interfaces so much thicker, than those found in laboratory experiments and
numerical simulations? For one thing, most lab and numerical experiments
have been initialized as two homogeneous layers separated by a very thin
interface which is allowed to grow under the influence of fingers. In the
ocean, the initial state is better-described as one of continuous stratification.
However, even when experiments are initialized with thick gradient
regions, they evolve toward thinner interfaces with
![]() fluxes across
them (Stern and Turner 1969; Linden 1978). This suggests that there is
some additional process in the ocean not present in these idealized
experiments which prevents thin interfaces from forming. Possible
candidates are finescale internal wave shear and strain fluctuations, and
intermittent shear-driven turbulence.
fluxes across
them (Stern and Turner 1969; Linden 1978). This suggests that there is
some additional process in the ocean not present in these idealized
experiments which prevents thin interfaces from forming. Possible
candidates are finescale internal wave shear and strain fluctuations, and
intermittent shear-driven turbulence.
e. interaction with internal-wave strain ![]()
Internal-wave vertical divergence
![]() would act to thicken and thin interfaces, modulating the fingering environment and
possibly leading to a rectified effect on fluxes, depending on the relative
timescales of the strain
would act to thicken and thin interfaces, modulating the fingering environment and
possibly leading to a rectified effect on fluxes, depending on the relative
timescales of the strain ![]() and finger adjustment. Stamp et al. (1998)
found a feedback that augmented the internal waves. However, this process has not
been explored an oceanic parameter regime.
and finger adjustment. Stamp et al. (1998)
found a feedback that augmented the internal waves. However, this process has not
been explored an oceanic parameter regime.
f. interaction with internal-wave vertical shear ![]()
Vertical shear
![]() should act to tilt square planform salt
fingers. Linden (1974) demonstrated in the lab and analytically (see also
Thangam et al. 1984) that, in steady shear Uz, fingers formed vertical
sheets
should act to tilt square planform salt
fingers. Linden (1974) demonstrated in the lab and analytically (see also
Thangam et al. 1984) that, in steady shear Uz, fingers formed vertical
sheets
![]() aligned with the shear. Linden reported the fluxes to be
unaltered by the presence of vertical shear.
aligned with the shear. Linden reported the fluxes to be
unaltered by the presence of vertical shear.
However, finescale vertical shear in the ocean is dominated by O(N)
near-inertial internal wave fluctuations. These rotate clockwise in time on
a timescale of f1 where
![]() is the Coriolis
frequency, and both clockwise and counterclockwise with depth. Near-inertial shear
will turn out of alignment with initially-aligned sheets, causing them to tilt over
on timescales comparable to the finger growth rate (Kunze 1990). Shear-
tilting may explain the nearly-horizontal 0.5-cm laminae consistently
observed with a shadowgraph (Laplacian of index of refraction
is the Coriolis
frequency, and both clockwise and counterclockwise with depth. Near-inertial shear
will turn out of alignment with initially-aligned sheets, causing them to tilt over
on timescales comparable to the finger growth rate (Kunze 1990). Shear-
tilting may explain the nearly-horizontal 0.5-cm laminae consistently
observed with a shadowgraph (Laplacian of index of refraction
![]() )
in
fingering-favorable parts of the ocean (Kunze et al. 1987; St. Laurent and
Schmitt 1997). These laminae appear to have horizontal scales consistent
with fastest-growing scales. Their small vertical scale would diffuse
away molecularly in
)
in
fingering-favorable parts of the ocean (Kunze et al. 1987; St. Laurent and
Schmitt 1997). These laminae appear to have horizontal scales consistent
with fastest-growing scales. Their small vertical scale would diffuse
away molecularly in ![]() minutes if it was temperature, and in
minutes if it was temperature, and in ![]() h if it
was salinity, indicating that it must be continuously produced in order to be
present in the ocean. Shear-tilting of growing fingers was argued to be a
plausible explanation. Kunze (1990) showed that the observed structure
could represent remnant shear-tilted salt microstructure just before it is
molecularly diffused away using the WKB wavenumber equation
h if it
was salinity, indicating that it must be continuously produced in order to be
present in the ocean. Shear-tilting of growing fingers was argued to be a
plausible explanation. Kunze (1990) showed that the observed structure
could represent remnant shear-tilted salt microstructure just before it is
molecularly diffused away using the WKB wavenumber equation
| (11) |
| (12) |
g. interaction with intermittent shear-driven turbulence
Turbulence produced by internal wave shear is an intermittent
process found in 5-10% of the stratified ocean interior. Linden (1971)
demonstrated that even very weak turbulence completely disrupts finger
fluxes. This was used by Kunze (1995) to argue that rapidly-growing
fingers at density ratios
![]() will be able to grow to their maximum
height (as determined by a finger Froude number-like constraint) without
being disturbed by turbulence. At higher density ratios, however,
intermittent turbulence arising every 10-20 buoyancy periods would limit
finger growth. This results in dramatically reduced fingering fluxes for
density ratios
will be able to grow to their maximum
height (as determined by a finger Froude number-like constraint) without
being disturbed by turbulence. At higher density ratios, however,
intermittent turbulence arising every 10-20 buoyancy periods would limit
finger growth. This results in dramatically reduced fingering fluxes for
density ratios
![]() (Fig. 10) and may explain why thermohaline
staircases are found in the ocean only for density ratios less than two. The
intermittency of turbulence following a water parcel is not well-known in
the ocean.
(Fig. 10) and may explain why thermohaline
staircases are found in the ocean only for density ratios less than two. The
intermittency of turbulence following a water parcel is not well-known in
the ocean.
REFERENCES
Carmack, E.C., K. Aagaard, J.H. Swift, R.W. Macdonald, F.A. McLaughlin, E.P. Jones, R.G. Perkin, J.N. Smith, K.M. Ellis and L.R. Kilius, 1998: Changes in temperature and tracer distributions within the Arctic Ocean: Results from the 1994 Arctic Ocean section. Deep-Sea Res., 45, submitted.
Fleury, M., and R. Lueck, 1991: Fluxes across a thermohaline interface. Deep-Sea Res., 38, 745-769.
Gargett, A.E., and R.W. Schmitt, 1982: Observations of salt fingers in the Central Waters of the eastern North Pacific. J. Geophys. Res., 87, 8017-8029.
Gregg, M.C., and T.B. Sanford, 1987: Shear and turbulence in thermohaline staircases. Deep-Sea Res., 34, 1689-1696.
Hebert, D., 1988: Estimates of salt-finger fluxes. Deep-Sea Res., 35, 1887-1901.
Holyer, J.Y., 1981: On the collective instability of salt fingers. J. Fluid Mech., 110, 195-207.
Holyer, J.Y., 1984: The stability of long, steady, two-dimensional slat fingers. J. Fluid Mech., 147, 169-185.
Howard, L.N., and G. Veronis, 1987: The salt-finger zone. J. Fluid Mech., 183, 1-23.
Howard, L.N., and G. Veronis, 1992: Stability of salt fingers with negligible diffusivity. J. Fluid Mech., 239, 511-522.
Huppert, H.E., and P.C. Manins, 1973: Limiting conditions for salt- fingering at an interface. Deep-Sea Res., 20, 315-323.
Joyce, T.M., 1982: Marginally-unstable salt fingers: Limits to growth. J. Mar. Res., 40 (Suppl.), 291-306.
Kelley, D.E., 1984: Effective diffusivities within oceanic thermohaline staircases. J. Geophys. Res., 89, 10,484-10,488.
Kunze, E., 1987: Limits on growing, finite-length salt fingers: A Richardson number constraint. J. Mar. Res., 45, 533-556.
Kunze, E., 1990: The evolution of salt fingers in inertial wave shear. J. Mar. Res., 48, 471-504.
Kunze, E., 1994: A proposed flux constraint for salt fingers in shear. J. Mar. Res., 52, 999-1016.
Kunze, E., 1995: Quantifying salt-fingering fluxes in the ocean. in Double-Diffusive Convection, A. Brandt and J. Fernando, Eds., AGU Geophysical Monograph 94, 313-320.
Kunze, E., A.J. Williams III and R.W. Schmitt, 1987: Optical microstructure in the thermohaline staircase. Deep-Sea Res., 34, 1697-1704.
Linden, P.F., 1971: Salt fingers in the presence of grid-generated turbulence. J. Fluid Mech., 49, 611-624.
Linden, P.F., 1973: On the structure of salt fingers. Deep-Sea Res., 20, 325-340.
Linden, P.F., 1974: Salt fingers in a steady shear flow. Geophys. Fluid Dyn., 6, 1-27.
Linden, P.F., 1978: The formation of banded salt-finger structure. J. Geophys. Res., 83, 2902-2912.
Lueck, R.G., 1987: Microstructure measurements in a thermohaline staircase. Deep-Sea Res., 34, 1677-1688.
Marmorino, G.O., 1987: Observations of small-scale mixing processes in the seasonal thermocline: Part I. Salt fingering. J. Phys. Oceanogr., 17, 1339-1347.
Marmorino, G.O., 1989: Substructure of oceanic salt-finger interfaces. J. Geophys. Res., 94, 4891-4904.
Marmorino, G.O., 1990: "Turbulent mixing" in a salt-finger interface. J. Geophys. Res., 95, 12,983-12,994.
Marmorino, G.O., W.K. Brown and W.D. Morris, 1987: Two- dimensional temperature structure in the C-SALT thermohaline staircase. Deep-Sea Res., 1667-1676.
McDougall, T.J., 1991: Interfacial advection in the thermohaline staircase east of Barbados. Deep-Sea Res., 38, 357-370.
McDougall, T.J., and J.R. Taylor, 1984: Flux measurements across a finger interface at low values of the stability ratio. J. Mar. Res., 42, 1-14.
Miles, J.W., and L.N. Howard, 1961: On the stability of heterogeneous shear flows. J. Fluid Mech., 10, 496-512.
Piacsek, S.A., and J. Toomre, 1980: Nonlinear evolution and structure of salt fingers. in Marine Turbulence, J.C.J. Nihoul, Ed., Elsevier, 193-219.
Schmitt, R.W., 1979a: Flux measurements in an interface. J. Mar. Res., 37, 419-436.
Schmitt, R.W., 1979b: The growth rate of supercritical salt fingers. Deep-Sea Res., 26A, 23-44.
Schmitt, R.W., 1994: Double diffusion in oceanography. Ann. Rev. Fluid Mech., 26, 255-285.
Schmitt, R.W., 1994: Triangular and asymmetric salt fingers. J. Phys. Oceanogr., 24, 855-860.
Schmitt, R.W., 1995: The ocean's salt fingers. Sci. Amer., 272(5), 50-55.
Schmitt, R.W., H. Perkins, J.D. Boyd and M.C. Stalcup, 1987: C-SALT: An investigation of the thermohaline staircase in the western tropical North Atlantic, Deep-Sea Res., 34, 1655-1666.
Shen, C.Y., 1989: The evolution of the double-diffusive instability: Salt fingers. Phys. Fluids A, 1, 829-844.
Shen, C.Y., 1993: Heat-salt finger fluxes across a density interface. Phys. Fluids A, 5, 2633-2643.
Shen, C.Y., 1995: Equilibrium salt-fingering convection. Phys. Fluids,
Shen, C.Y., and R.W. Schmitt, 1995: The salt-finger wavenumber spectrum. in Double-Diffusive Convection, A. Brandt and J. Fernando, Eds., AGU Monograph 94, 305-312.
Simpson, J.H., M.R. Howe, N.C.G. Morris and J. Stratford, 1979: Velocity shear on the steps below the Mediterranean outflow. Deep-Sea Res., 26A, 1381-1386.
Stamp, A.P., G. Hughes, R.W. Griffiths and R.I. Nokes, 1998: Coherent circulation due to coupling of double-diffusive convection and interfacial waves. J. Fluid Mech., submitted.
Stern, M.E., 1960: The "salt-fountain" and thermohaline convection. Tellus, 12, 172-175.
Stern, M.E., 1969: Collective instability of salt fingers. J. Fluid Mech., 35, 209-218.
Stern, M.E., 1975: Ocean Circulation Physics. Academic Press, NY, 191-203.
Stern, M.E., 1976: Maximum buoyancy-flux across a salt-finger interface. J. Mar. Res., 34, 95-110.
Stern, M.E., and J.S. Turner, 1969: Salt fingers and convecting layers. Deep-Sea Res., 16, 497-511.
Taylor, J.R., and P. Bucens, 1989: Laboratory experiments on the structure of salt fingers. Deep-Sea Res., 36, 1675-1704.
Thangam, S., A. Zebib and C.F. Chen, 1984: Salt-finger convection in shear flow. Phys. Fluids, 27, 804-811.
Turner, J.S., 1967: Salt fingers across a density interface. Deep-Sea Res., 14, 599-611.
FIGURE CAPTIONS
Figure EK1: Contours of salt-finger growth rate normalized by buoyancy
frequency ![]() for parameter values typical of the high-gradient interfaces
in the thermohaline staircase east of Barbados (Table EK1) as a function of
finger wavelength
for parameter values typical of the high-gradient interfaces
in the thermohaline staircase east of Barbados (Table EK1) as a function of
finger wavelength ![]() and background density ratio
and background density ratio
![]() .
Growth rates are negative (decay) for wavelengths
.
Growth rates are negative (decay) for wavelengths
![]() cm
and positive at larger wavelengths. They exceed the buoyancy frequency
cm
and positive at larger wavelengths. They exceed the buoyancy frequency
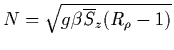 only at very low density ratios. The dotted curve
displays the wavelength of maximum growth rate.
only at very low density ratios. The dotted curve
displays the wavelength of maximum growth rate.
Figure EK2: Contours of flux ratio
![]() as a
function of finger wavelength
as a
function of finger wavelength ![]() and density ratio
and density ratio ![]() .
The dotted curve
shows the wavelength of maximum growth rate as a function of density ratio. The
flux ratio RF increases from 0 for vanishing growth rate to 0.85 for
density ratios
.
The dotted curve
shows the wavelength of maximum growth rate as a function of density ratio. The
flux ratio RF increases from 0 for vanishing growth rate to 0.85 for
density ratios
![]() and wavelengths
and wavelengths
![]() cm.
cm.
Figure EK3: Salt-finger flux ratio
![]() vs density ratio
vs density ratio
![]() .
Symbols are from laboratory and numerical simulation estimates, the
solid curve for theoretical fastest-growing fingers and the dashed curve for
steady
.
Symbols are from laboratory and numerical simulation estimates, the
solid curve for theoretical fastest-growing fingers and the dashed curve for
steady
![]() fingers.
fingers.
Figure EK4: An example of numerical simulation of growing salt fingers in a thin interface (Shen 1993). The resulting structure does not resemble the tall thin fingers of theoretical treatments but quickly becomes nearly isotropic and blob-like.
Figure EK5: Theoretical wavelengths ![]() as a function of density
ratio
as a function of density
ratio ![]() for fastest-growing (solid) and steady (dashed) fingers using typical
properties of interfaces in the thermohaline staircase east of Barbados
(Table EK1).
for fastest-growing (solid) and steady (dashed) fingers using typical
properties of interfaces in the thermohaline staircase east of Barbados
(Table EK1).
Figure EK6: Maximum theoretical finger growth rates ![]() (solid) as a
function of density ratio
(solid) as a
function of density ratio ![]() for interfaces in the thermohaline staircase east
of Barbados (Table EK1). Also shown are buoyancy frequencies N
(dashed) and molecular viscous and diffusive timescales (dotted).
for interfaces in the thermohaline staircase east
of Barbados (Table EK1). Also shown are buoyancy frequencies N
(dashed) and molecular viscous and diffusive timescales (dotted).
Figure EK7: Theoretical heat (dashed), salt (dotted) and total (solid)
buoyancy-fluxes as a function of density ratio ![]() .
The maximum finger
amplitude is assumed to be constrained by a critical finger Froude number
.
The maximum finger
amplitude is assumed to be constrained by a critical finger Froude number
![]() where the vertically-sheared horizontal velocity of the
usual gradient Froude number has been replaced with the horizontally-
sheared vertical velocity between adjacent fingers. The negative of the
total buoyancy-flux is shown. The upper panel assumes an interface
thickness li of 2 m, consistent with observed values. The central panel
assumes that the interface thickness li is identical to the maximum finger
height
where the vertically-sheared horizontal velocity of the
usual gradient Froude number has been replaced with the horizontally-
sheared vertical velocity between adjacent fingers. The negative of the
total buoyancy-flux is shown. The upper panel assumes an interface
thickness li of 2 m, consistent with observed values. The central panel
assumes that the interface thickness li is identical to the maximum finger
height
![]() ,
producing interface thicknesses of
,
producing interface thicknesses of ![]() (10 cm) and higher
fluxes as a result. The bottom panel normalizes these fluxes by the lab
(10 cm) and higher
fluxes as a result. The bottom panel normalizes these fluxes by the lab
![]() flux laws and compares the salt-flux (dotted) with values from
laboratory and numerical experiments (symbols). The model reproduces
the observed values for density ratios
flux laws and compares the salt-flux (dotted) with values from
laboratory and numerical experiments (symbols). The model reproduces
the observed values for density ratios
![]() but underestimates fluxes at
low density ratios
but underestimates fluxes at
low density ratios ![]() .
.
Figure EK8: Flux ratio Rf (a),
![]() flux law coefficient
c
(b) and Stern number A (c) as a function of density ratio from numerical
simulations (solid diamonds) and lab experiments (other symbols) (from Shen 1993).
The laboratory and numerical numbers are consistent with each other and
indicate that the Stern number is not an invariant.
flux law coefficient
c
(b) and Stern number A (c) as a function of density ratio from numerical
simulations (solid diamonds) and lab experiments (other symbols) (from Shen 1993).
The laboratory and numerical numbers are consistent with each other and
indicate that the Stern number is not an invariant.
Figure EK9: Temperature Cox number CT versus vertical temperature-
gradient
![]() in interfaces of the thermohaline staircase east of
Barbados. Data are from (a) a towed microscale conductivity cell (Marmorino 1989)
and (b) a towed microthermiistor (Fleury and Lueck 1991). The solid dots
in (a) denote the mean of the distribution, the open circles the mode. Only
the means are displayed in (b). Both data sets display mean Cox numbers
in interfaces of the thermohaline staircase east of
Barbados. Data are from (a) a towed microscale conductivity cell (Marmorino 1989)
and (b) a towed microthermiistor (Fleury and Lueck 1991). The solid dots
in (a) denote the mean of the distribution, the open circles the mode. Only
the means are displayed in (b). Both data sets display mean Cox numbers
![]() .
The Stern or finger Froude number predicts a Cox
number of
.
The Stern or finger Froude number predicts a Cox
number of ![]() ,
independent of temperature-gradient.
,
independent of temperature-gradient.
Figure EK10: Theoretical finger salt diffusivities KS as a function of
density ratio ![]() in the thermohaline staircase east of Barbados. The solid
curve assumes a finger Froude number constraint
in the thermohaline staircase east of Barbados. The solid
curve assumes a finger Froude number constraint
![]() ,
the
thin dashed curve a mixed finger/wave Froude number
Uzwy/N2 = 2.0 with
wave shear
Uz = 0.6N, and the thick dashed curve the appropriate
diffusivity for gradients smoothed over a staircase. The dotted curves are
diffusivities where finger growth is halted by intermittent internal-wave-
driven turbulence every 10 buoyancy periods. A plausible scenario for the
ocean is that (i) at high density ratios
,
the
thin dashed curve a mixed finger/wave Froude number
Uzwy/N2 = 2.0 with
wave shear
Uz = 0.6N, and the thick dashed curve the appropriate
diffusivity for gradients smoothed over a staircase. The dotted curves are
diffusivities where finger growth is halted by intermittent internal-wave-
driven turbulence every 10 buoyancy periods. A plausible scenario for the
ocean is that (i) at high density ratios
![]() ,
finger growth is inhibited
by turbulence rather than self secondary instability (dotted curves) while,
(ii) for low density ratios
,
finger growth is inhibited
by turbulence rather than self secondary instability (dotted curves) while,
(ii) for low density ratios
![]() ,
finger countergradient buoyancy-fluxes
overcome turbulent downgradient buoyancy-fluxes (stippling) and
staircases form, producing high-gradient interfaces and amplifying the
fluxes (thick dashed). At intermediate density ratios, finger diffusivities
will lie between the thick solid and thin dashed curves depending on the
strength of the internal wave shear Uz. The resulting curve resembles
Fig. 5 of Schmitt (1981), albeit a factor of 30 lower.
,
finger countergradient buoyancy-fluxes
overcome turbulent downgradient buoyancy-fluxes (stippling) and
staircases form, producing high-gradient interfaces and amplifying the
fluxes (thick dashed). At intermediate density ratios, finger diffusivities
will lie between the thick solid and thin dashed curves depending on the
strength of the internal wave shear Uz. The resulting curve resembles
Fig. 5 of Schmitt (1981), albeit a factor of 30 lower.