3.2 The CANDIE Forward Time Integration

In the A-grid formulation the temperature and
salinity are volume averages for a cell and we interpolate the A-grid
velocities to the C-grid cell faces in order to deal with the
conservation equations. The basic approach goes as follows. Assume we
start out knowing the velocity at both the C-grid (cell face) and
the temperature, salinity and velocity at the A-grid (volume
average) locations. Suppose further that these quantities are known
at two successive times
to and 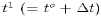 . Using
standard centered differences in space and a leapfrog scheme in time,
the temperature T and salinity S
are updated to time level
. Using
standard centered differences in space and a leapfrog scheme in time,
the temperature T and salinity S
are updated to time level 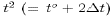 .
Similarly, the A-grid velocity components U0 and V0 from time level
to can be updated to the time level t2 for the effects of advection,
diffusion and Coriolis acceleration. However, the
surface pressure is not yet known at the time level t1, so only an
approximation to the pressure driven acceleration can be determined.
This approximation is based on the
surface pressure field at the initial time level to and the density
variations at the time level t1. The correction due to the change in
surface pressure between to and t1 must be added on later.
.
Similarly, the A-grid velocity components U0 and V0 from time level
to can be updated to the time level t2 for the effects of advection,
diffusion and Coriolis acceleration. However, the
surface pressure is not yet known at the time level t1, so only an
approximation to the pressure driven acceleration can be determined.
This approximation is based on the
surface pressure field at the initial time level to and the density
variations at the time level t1. The correction due to the change in
surface pressure between to and t1 must be added on later.
How does DieCAST determine the change in surface pressure between
to and t1? Mathematical details are given in Appendix A, but the
basic approach is actually quite simple. Given that the velocity
field is non-divergent at time to, the idea is to determine the
surface pressure at time t1 that is required to insure that the
velocity field at time t2 remains non-divergent. Any imbalances in
continuity associated with errors in the velocity field must be
balanced by changing the velocity. Because all other effects have
already been accounted for, these velocity changes must be driven by
the gradients in the surface pressure difference 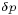 between
the time levels to and t1. To determine an equation for
between
the time levels to and t1. To determine an equation for 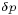 ,
we first write the horizontal velocity components in terms of the
previously estimated values at t2 plus the correction associated with
the unknown
,
we first write the horizontal velocity components in terms of the
previously estimated values at t2 plus the correction associated with
the unknown 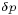 . Forming the depth-integrated continuity equation
now results in a simple 2D elliptic equation for
. Forming the depth-integrated continuity equation
now results in a simple 2D elliptic equation for 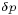 .
After solving this equation for
.
After solving this equation for 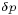 the horizontal velocity
components are adjusted for the additional pressure driven acceleration
and the vertical velocity is updated using the 3D continuity equation.
the horizontal velocity
components are adjusted for the additional pressure driven acceleration
and the vertical velocity is updated using the 3D continuity equation.
The above paragraph describes the basic idea. However, this approach
assumes that the velocity is known at the C-grid locations in order
to determine the continuity errors that need to be corrected, but the
velocity updates from to to t2 were actually done at the A-grid
locations. Thus, to apply this methodology, one must interpolate the
velocities from the A-grid to the C-grid. The velocity field is
then corrected on the C-grid and the changes must then be
interpolated back to the A-grid. These technical details are
relegated to Appendix A. However, it should be noted that the C-grid
velocities resulting from this approach precisely satisfy the
continuity equation and that the Coriolis terms do not suffer from the
need for horizontal interpolations.
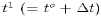 . Using
standard centered differences in space and a leapfrog scheme in time,
the temperature T and salinity S
are updated to time level
. Using
standard centered differences in space and a leapfrog scheme in time,
the temperature T and salinity S
are updated to time level 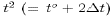 .
Similarly, the A-grid velocity components U0 and V0 from time level
to can be updated to the time level t2 for the effects of advection,
diffusion and Coriolis acceleration. However, the
surface pressure is not yet known at the time level t1, so only an
approximation to the pressure driven acceleration can be determined.
This approximation is based on the
surface pressure field at the initial time level to and the density
variations at the time level t1. The correction due to the change in
surface pressure between to and t1 must be added on later.
.
Similarly, the A-grid velocity components U0 and V0 from time level
to can be updated to the time level t2 for the effects of advection,
diffusion and Coriolis acceleration. However, the
surface pressure is not yet known at the time level t1, so only an
approximation to the pressure driven acceleration can be determined.
This approximation is based on the
surface pressure field at the initial time level to and the density
variations at the time level t1. The correction due to the change in
surface pressure between to and t1 must be added on later.

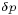 between
the time levels to and t1. To determine an equation for
between
the time levels to and t1. To determine an equation for 



