

where u,v,w are the east
and
where
Under the hydrostatic approximation (3), the pressure field
at depth z can be expressed in terms of the pressure at the rigid
upper surface, ps, plus that due to the fluid between the rigid lid
and the depth z:
Lateral boundary conditions are required to close the above governing
equations. No normal flow across solid boundaries is imposed and the
component of horizontal velocity tangent to solid walls satisfies
either free-slip or no-slip boundary conditions. In the case of
free-slip boundary conditions the tangential stress at vertical
boundaries is set to zero, and for the no-slip boundary condition, the
tangential velocity at the boundary is set to zero. Note that since
the real bathymetry is represented by a series of steps in the Z-level
model, lateral boundary conditions are required not only at the coast,
but also at all submerged vertical boundaries.
The boundary conditions for the vertical velocity component w are
based on the rigid-lid approximation and the condition of no normal
flow at the bottom. For general topography these conditions can be
expressed as
where the subscripts 0 and -h indicate evaluation at
the sea surface z=0 and at the sea bottom z=-h, respectively.
Integrating the continuity equation (4), and using
(11) gives
and substituting (12) into (13), we obtain the
depth-integrated continuity equation:
Equation (14) holds for general topography and is valid in
both z and sigma coordinate formulations. Note that for the step-like
topography of Z-coordinate models, h is uniform over each individual
grid cell and there is no flow through solid boundaries; hence
A.1 The Governing Equations
We consider the three dimensional (3D) primitive equations for an
incompressible, stratified fluid using the rigid-lid, Boussinesq, and
hydrostatic approximations. They are essentially the same as those
considered by Dietrich [1992], except that spherical polar
coordinates are used here. 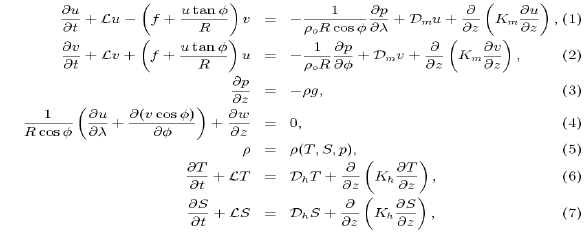
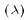 , north
, north 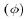 , and vertical
(z) components of the velocity, p is pressure,
, and vertical
(z) components of the velocity, p is pressure, 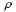 ; is density,
T and S are potential temperature and salinity, Km and Kh
are vertical eddy viscosity and diffusivity coefficients, f is the
Coriolis parameter,
; is density,
T and S are potential temperature and salinity, Km and Kh
are vertical eddy viscosity and diffusivity coefficients, f is the
Coriolis parameter,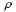 o is a reference density, R and g are
the Earth's radius and gravitational acceleration,
o is a reference density, R and g are
the Earth's radius and gravitational acceleration, 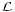 is an
advection operator defined as
is an
advection operator defined as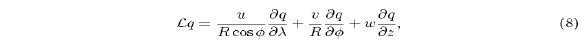
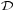 m and
m and 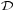 h are diffusion operators defined as
h are diffusion operators defined as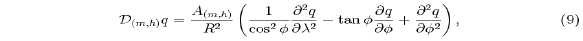
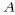 m and
m and 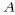 h are horizontal eddy viscosity and diffusivity
coefficients, respectively.
h are horizontal eddy viscosity and diffusivity
coefficients, respectively.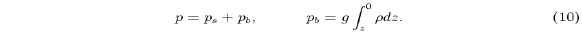
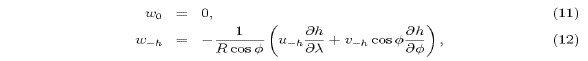
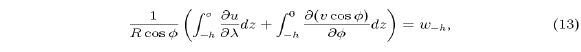
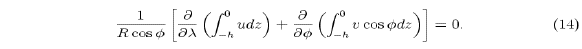
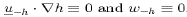 .
.




