

Both DieCAST and CANDIE are similar to the GFDL model, most notably in
the use of Cartesian coordinates and the rigid lid
approximation. However, unlike the GFDL model (referred to the
tradition version of the Modular Ocean Model) uses a volume transport
streamfunction, both DieCAST and CANDIE are formulated in terms of the
surface pressure. The main advantages of using a pressure formulation
are the increased ease with which islands are handled, and the reduced
numerical sensitivity to depth variations. The latter attribute is due
to the appearance of 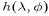 (rather than
(rather than
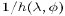 as in the stream function formulation) in the
differential equation determining the surface pressure, and reduces
the need to smooth the model bottom topography to maintain numerical
stability [e.g. Dukowicz et al., 1993]. Again, we emphasize that in
all references to the GFDL model, we are referring to the particular
version used in the test cases presented by HB, which uses the
streamfunction formulation. Madala and Piacsek [1977], Killworth et al.
[1991], Dukowicz et al. [1993], Dukowicz and Smith[1994] and
Pacanowski [1996] have each reformulated the GFDL model using
different pressure formulations and it would be of interest to explore
how these models perform on Haidvogel and Beckmann's test cases.
However, our interest here is in the approach used by Dietrich which
is distinct from each of those mentioned above. This approach is
presented below.
as in the stream function formulation) in the
differential equation determining the surface pressure, and reduces
the need to smooth the model bottom topography to maintain numerical
stability [e.g. Dukowicz et al., 1993]. Again, we emphasize that in
all references to the GFDL model, we are referring to the particular
version used in the test cases presented by HB, which uses the
streamfunction formulation. Madala and Piacsek [1977], Killworth et al.
[1991], Dukowicz et al. [1993], Dukowicz and Smith[1994] and
Pacanowski [1996] have each reformulated the GFDL model using
different pressure formulations and it would be of interest to explore
how these models perform on Haidvogel and Beckmann's test cases.
However, our interest here is in the approach used by Dietrich which
is distinct from each of those mentioned above. This approach is
presented below.
Using forward time stepping for horizontal diffusion terms, centered time stepping for advection and pressure variations, backward (or fully implicit) time stepping for vertical diffusion, and either centered or backward time stepping for the Coriolis term, the time discretization of (1), (2), (6) and (7) can be written as
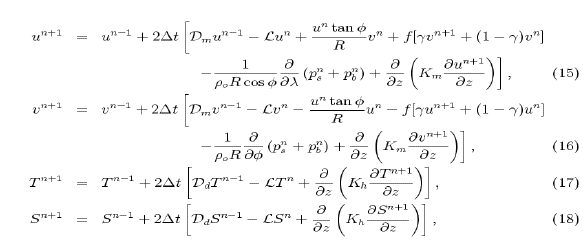
where 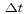 is the time step and superscripts n-1, n and n+1
represent the values of quantities at the corresponding time steps.
The quantity
is the time step and superscripts n-1, n and n+1
represent the values of quantities at the corresponding time steps.
The quantity 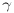 is a measure of implicitness for the Coriolis
term:
is a measure of implicitness for the Coriolis
term: 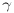 = 0 gives centered (leap-frog) time differencing and
= 0 gives centered (leap-frog) time differencing and
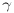 = 1 gives backward (fully implicit) treatment of the Coriolis
term. Dietrich et al. [1987] noted that, when the Ekman layer is
resolved, an extremely short time step would be required if an
explicit scheme were used for the vertical diffusion terms. To avoid
this undesirable restriction, while maintaining an accurate
representation of the Ekman layer dynamics, Dietrich et al. [1990]
suggested that both the Coriolis and the vertical diffusion terms
should be treated implicitly. The equations derived below allow for
either implicit or explicit treatment of the Coriolis terms, but treat
the vertical mixing in both the momentum and tracer equations
implicitly.
= 1 gives backward (fully implicit) treatment of the Coriolis
term. Dietrich et al. [1987] noted that, when the Ekman layer is
resolved, an extremely short time step would be required if an
explicit scheme were used for the vertical diffusion terms. To avoid
this undesirable restriction, while maintaining an accurate
representation of the Ekman layer dynamics, Dietrich et al. [1990]
suggested that both the Coriolis and the vertical diffusion terms
should be treated implicitly. The equations derived below allow for
either implicit or explicit treatment of the Coriolis terms, but treat
the vertical mixing in both the momentum and tracer equations
implicitly.
Clearly, since the Coriolis term may include a fully implicit contribution and the vertical diffusion is always treated implicitly, the state variables cannot be updated in the straightforward manner implied by the above equations. In practice, the updating is done through a sequence of steps equivalent to solving the above equations in combination with the continuity and hydrostatic equations at appropriate time levels.
Let us rewrite un+1, vn+1, Tn+1 and Sn+1 in terms of a set of trial variables:
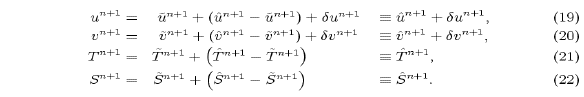
where the initial trial fields 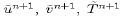 and
and 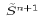 are updated to include the effects of horizontal
diffusion (forward), nonlinearity (centered), the pressure gradient
force (centered baroclinic and forward surface contributions), and
the contribution to the Coriolis force based on centered differencing.
are updated to include the effects of horizontal
diffusion (forward), nonlinearity (centered), the pressure gradient
force (centered baroclinic and forward surface contributions), and
the contribution to the Coriolis force based on centered differencing.
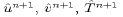 and
and 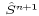 include the
additional effects of vertical diffusion (backward) and the
contribution to the Coriolis force based on backward differencing.
Finally,
include the
additional effects of vertical diffusion (backward) and the
contribution to the Coriolis force based on backward differencing.
Finally, 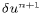 and
and 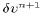 represent the corrections to
the velocity components required to allow for a time-centered surface
pressure.
represent the corrections to
the velocity components required to allow for a time-centered surface
pressure.
The initial trial fields 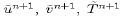 and
and 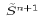 are given by
are given by
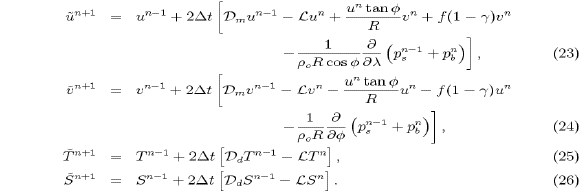
Each of the terms on the right sides of (23)-(26)
are expressed in terms of previously determined state variables and
hence are trivially calculated. Note the appearance of 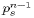 rather than
rather than 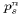 on the right hand sides of (23) and
(24). The quantity
on the right hand sides of (23) and
(24). The quantity 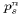 is not yet known, but it
will be determined and properly accounted for in the final step of
the solution procedure.
is not yet known, but it
will be determined and properly accounted for in the final step of
the solution procedure.
The advanced trial fields 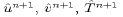 and
and
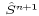 are then determined by updating
are then determined by updating 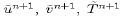 and
and 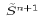 to give the best current estimates of the
effects of vertical diffusion and Coriolis:
to give the best current estimates of the
effects of vertical diffusion and Coriolis:
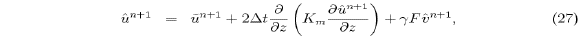
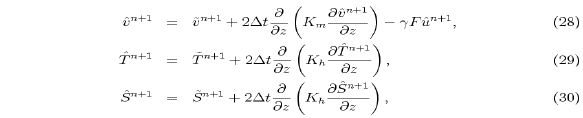
where  . Note that we have used
. Note that we have used  and
and 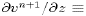
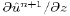 in the vertical diffusion terms on the right sides
of (27) and (28), since the pressure
correction terms,
in the vertical diffusion terms on the right sides
of (27) and (28), since the pressure
correction terms, 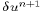 and
and 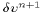 , are depth-independent (see (33) and (34)).
Also note that
, are depth-independent (see (33) and (34)).
Also note that 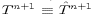 and
and 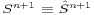 (see (21) and (22)) have been used in the
vertical diffusion terms on the right hand sides of (29) and
(30).
(see (21) and (22)) have been used in the
vertical diffusion terms on the right hand sides of (29) and
(30).
At this point, 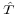 and
and 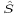 are completely updated, but
are completely updated, but 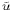 and
and
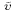 are based on the use of
are based on the use of 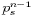 rather than
rather than 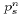 on the
right sides of (23) and (24), and the effect spills
over into (27) and (28) through the use of
on the
right sides of (23) and (24), and the effect spills
over into (27) and (28) through the use of
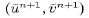 on the right sides of these equations. It
remains to adjust the pressure terms to the time level n and update
the velocities appropriately in order to achieve a fully time centered
pressure formulation.
on the right sides of these equations. It
remains to adjust the pressure terms to the time level n and update
the velocities appropriately in order to achieve a fully time centered
pressure formulation.
Subtracting (27) from (15), then using
(23) to eliminate 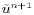 , and performing the
corresponding operations on (16),(24) and
(28) gives
, and performing the
corresponding operations on (16),(24) and
(28) gives
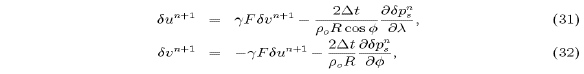
in which 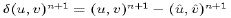 and
and ![]() . It follows that
. It follows that
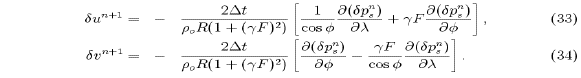
Note that 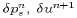 and
and 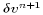 are all
independent of z. Hence they make no contribution to the vertical
diffusion terms which are thus fully accounted by (27) and
(28).
are all
independent of z. Hence they make no contribution to the vertical
diffusion terms which are thus fully accounted by (27) and
(28).
Substitution of (19) and (20) into (14) and then using (33) and (34) gives
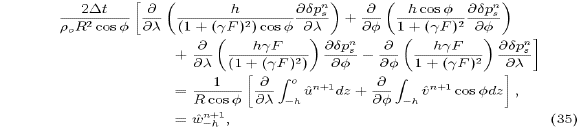
where the final equality is a convenient shorthand notation: the
penultimate form is used in all numerical calculations. Note that
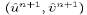 does not in general satisfy the
depth-integrated continuity equation. Therefore
does not in general satisfy the
depth-integrated continuity equation. Therefore 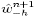 is not always zero, which leads non-zero corrections
is not always zero, which leads non-zero corrections 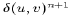 and
and 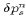 .
.
Equation (35) is the general equation determining the surface
pressure correction 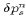 . For the special case
. For the special case 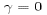 (centered Coriolis), this equation simplifies to
(centered Coriolis), this equation simplifies to
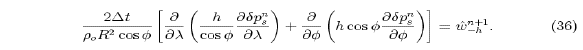
Equations (35) and (36) are forced 2D elliptic
equations for the surface pressure correction 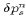 , with the
forcing determined by the net divergence (or convergence) implied by
the advanced trial horizontal velocity field
, with the
forcing determined by the net divergence (or convergence) implied by
the advanced trial horizontal velocity field 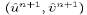 over each vertical water column. Equation (35) or
(36) determines the change in the surface pressure required
to adjust the vertical velocity at the bottom to zero, as required by
the step-like bottom topography, and is solved subject to the normal
gradient of pressure being zero on the boundaries (corresponding, from
(31) and (32), to having no normal velocity through
the boundaries of the model domain).
over each vertical water column. Equation (35) or
(36) determines the change in the surface pressure required
to adjust the vertical velocity at the bottom to zero, as required by
the step-like bottom topography, and is solved subject to the normal
gradient of pressure being zero on the boundaries (corresponding, from
(31) and (32), to having no normal velocity through
the boundaries of the model domain). 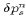 has been
determined from (35) or (36), the barotropic
horizontal velocity corrections
has been
determined from (35) or (36), the barotropic
horizontal velocity corrections 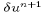 and
and 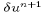 are
determined by (33) and (34). Note that while the
pressure is fully updated only to the time level n, the velocity,
temperature and salinity are each fully updated to the time level
n+1, as required by the above scheme.
are
determined by (33) and (34). Note that while the
pressure is fully updated only to the time level n, the velocity,
temperature and salinity are each fully updated to the time level
n+1, as required by the above scheme.
It is of significance that the above equation for the surface pressure
is linear. All nonlinear effects are included through the forcing term
which is fully determined at the central time level n so that no
iterations are required. As a consequence, the surface pressure can
be determined very efficiently using standard routines for elliptic
equations. Also note that the block implicit relaxation (BIR)
technique is used in both DieCAST and CANDIE to determine the surface
pressure correction 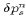 . The BIR technique was originally
developed by Dietrich et al. [1975] and later modified by Madala
[1978]. Roache [1995] discusses this computationally efficient and
numerically stable elliptic marching method in sum detail.
. The BIR technique was originally
developed by Dietrich et al. [1975] and later modified by Madala
[1978]. Roache [1995] discusses this computationally efficient and
numerically stable elliptic marching method in sum detail.
In summary, each time step proceeds as follows. We first determine
the baroclinic contribution pb to the pressure field at time level
n and add it to the surface pressure from time level n-1 to give
an initial estimate of the pressure field at time level n. The
initial trial fields 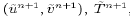 , and
, and
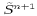 are determined to allow for the pressure gradient,
diffusive horizontal fluxes, advection and an estimate of the Coriolis
force based on the state variables at the previous two time steps. We
then calculate the advanced trial fields
are determined to allow for the pressure gradient,
diffusive horizontal fluxes, advection and an estimate of the Coriolis
force based on the state variables at the previous two time steps. We
then calculate the advanced trial fields 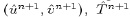 and
and ![]() to include vertical diffusion and any
implicit contribution to the Coriolis terms. The surface pressure
correction
to include vertical diffusion and any
implicit contribution to the Coriolis terms. The surface pressure
correction 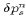 is then determined to eliminate the depth
integrated horizontal divergence of
is then determined to eliminate the depth
integrated horizontal divergence of 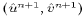 over each
water column. After numerically solving the governing 2D elliptic
equation for
over each
water column. After numerically solving the governing 2D elliptic
equation for 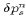 , the barotropic velocity corrections
, the barotropic velocity corrections 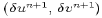 are readily calculated through (33)
and (34). Adding these velocity corrections to
are readily calculated through (33)
and (34). Adding these velocity corrections to
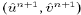 yields the total horizontal velocity
components
yields the total horizontal velocity
components 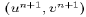 at the end of the time step. The
vertical velocity component
at the end of the time step. The
vertical velocity component 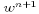 is then determined at each
Z-level by the horizontal divergence of
is then determined at each
Z-level by the horizontal divergence of 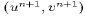 through
the continuity equation (4).
through
the continuity equation (4).




